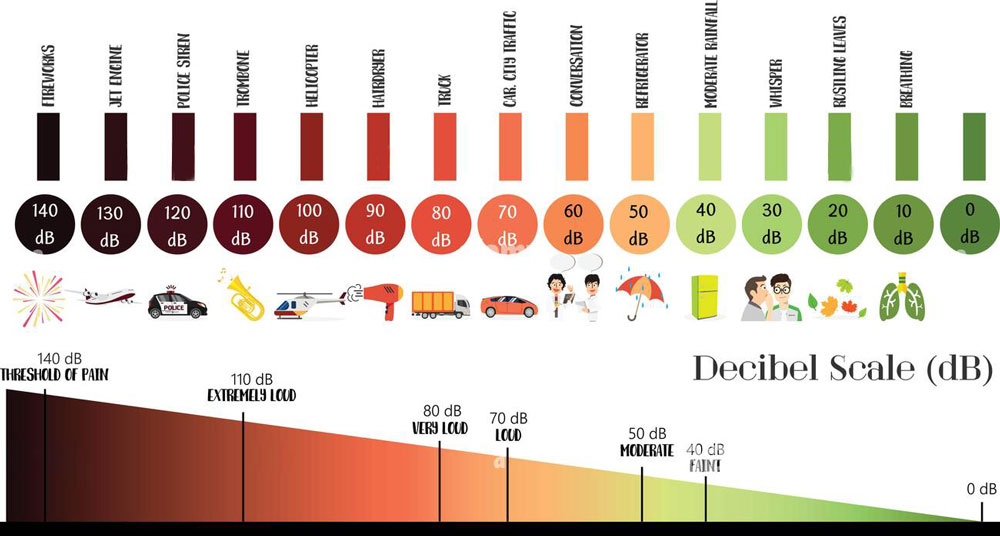
Âm thanh rất lớn – nhưng tải trọng và mức độ âm thanh thay đổi như thế nào khi bạn di chuyển ra xa hơn? Rõ ràng là nó nhận được ít hơn nhưng ít hơn bao nhiêu?
1. Mức âm thanh, cường độ âm
Mức cường độ âm được tính bằng Wm-2 và phép so sánh giữa hai âm có cường độ I và Io được tính bằng decibel theo công thức:
Decibel level = 10log(I/Io)
Ví dụ, sử dụng ngưỡng nghe có cường độ Io =10-12 Wm-2 thì chúng ta có thể tính toán mức decibel của âm thanh có cường độ 10-6 Wm-2.
Mức decibel = 10log (10-6 / 10-12) = 10log (106) = 60 dB về cường độ ở tai của hai người đang trò chuyện bình thường.
Tuy nhiên, ví dụ với những người có ngưỡng nghe 100 dB. Sử dụng công thức sau đó, có thể tính ra cường độ âm thanh mà tôi nghe thấy là:
Mức decibel = 10log (I / 10-12) = 100
Do đó: 1010 = I / 10-12 và do đó I = 1010x10-12 = 10-2 Wm-2.
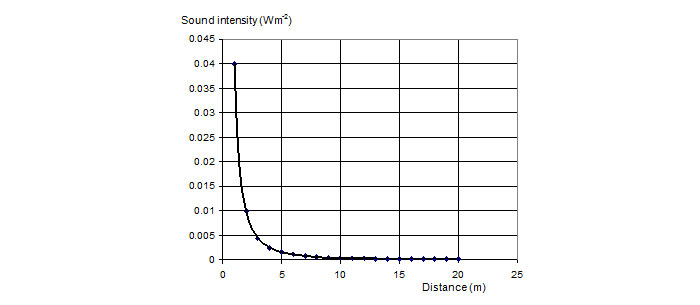
Tuy nhiên cường độ âm thanh sẽ giảm theo bình phương nghịch đảo của khoảng cách.
Cường độ ở khoảng cách d1 / Cường độ ở khoảng cách
Vậy người ở xa hơn rất nhiều ở đầu phòng bên kia thì sao? Mức độ âm thanh rõ ràng là ít hơn ở đây (để dễ hiểu, chúng tôi sẽ bỏ qua sự phản xạ từ các bức tường trong phòng).
Nói cách khác, nếu tôi cách nhóm 2m và bạn cách đó 20 m thì bạn sẽ phải chịu cường độ âm thanh 10-2 x (22/202) = 10-4 Wm-2 (một phần trăm cường độ âm thanh của tai tôi) và mức decibel 10log (10-4 / 10-12) = 80 dB – vẫn là tiếng ồn của hệ thống âm thanh nổi lớn.
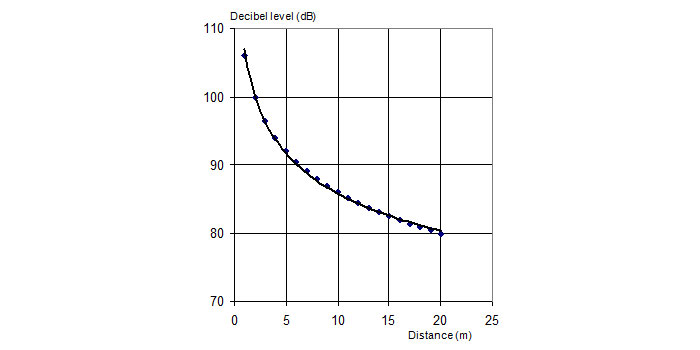
2. Tăng gấp đôi khoảng cách giữa người nghe và nguồn âm thanh sẽ làm giảm mức decibel chỉ hơn 6 dB.
Điều này được tính như sau: Cường độ được giảm xuống 1/4 so với ban đầu và do đó decibel thay đổi = 10log (1/4) = -6,02 dB. Dấu trừ có nghĩa là mức decibel giảm. Khoảng cách giảm sẽ dẫn đến sự gia tăng mức decibel, tạo ra một dấu cộng cho sự thay đổi decibel.
Đồ thị dưới đây biểu thị sự biến thiên của cả cường độ mức âm và mức decibel với khoảng cách từ nguồn âm lấy mức decibel là 80 dB ở 20 m.